Understanding P-Value in Research

Table of Contents

What is P-value in Research?

P-value is a valid outcome to check the level of significance in statistical analysis.
P-value stands for ‘Probability value’
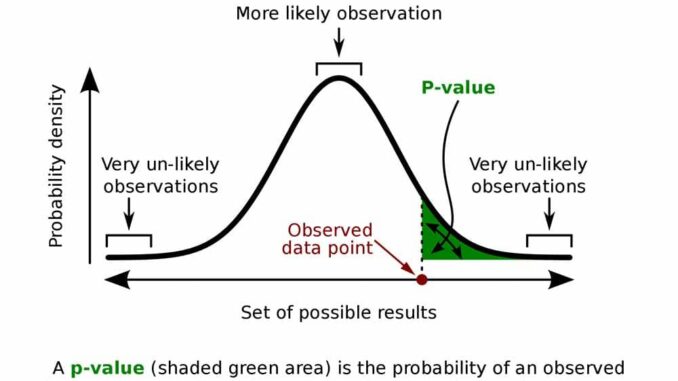
A p-value is the probability of obtaining test results at least as extreme as the observed results, assuming that the null hypothesis is true.
It is also known as the “observed significance level” for the test hypothesis.
In simpler terms, it quantifies the evidence against the null hypothesis.
The number that lies between O and 1 are the P-value and they are understood in the following way:
A small p-value (typically ≤ 0.05) specifies solid proof in contrast to the null hypothesis and reject the null hypothesis.
A large p-value (> 0.05) specifies fragile indication in contrast to the null hypothesis and be unsuccessful to reject the null hypothesis.
P-value very close to the endpoint (0.05) are reflected to be marginal (could go either way).

The Role of P-value in Hypothesis Testing

Hypothesis testing involves formulating two competing hypotheses:
- Null Hypothesis (H₀): Assumes no effect or no significant difference.
- Alternative Hypothesis (H₁): Assumes there is an effect or a significant difference.
P-value plays a vital role to draw conclusions of the research or hypothesis.
P-value is used to detect the relationship between two or more variables whether they are inter-related with each other or not during hypothesis testing.
It is calculated with various statistical software in order to check the level of significance.

Interpretation of P-value in Hypothesis Testing

If a P-value is small i.e. less than 0.05 (the predetermined significance level), then it is significant or provides strong proof, which means there is a relationship between variables
If a P-value is more than 0.05 then it is not significant, in result absence of a relationship between the variables.
The margin value to determine the significant level may not be the same as many researchers have their own perspective to use different levels of significance while examining the question

Common Significance Thresholds

The significance level, denoted by alpha (α), is the threshold for determining statistical significance. Common alpha levels include:

0.05 (5%): Standard threshold for statistical significance.
0.01 (1%): Indicates stronger evidence against the null hypothesis.
0.10 (10%): Used in exploratory research where a higher tolerance for Type I error is acceptable.

It’s important to note that these thresholds are conventions and not absolute rules. The choice of alpha should be based on the context of the study and the consequences of Type I and Type II errors.

Conceptual Calculation of P-value

While the mathematical computation of p-values can be complex, the conceptual steps are as follows:

Assume the Null Hypothesis is True: Start with the assumption that there is no effect or difference.
Collect Data and Calculate Test Statistic: Use appropriate statistical tests (e.g., t-test, chi-square test) to calculate a test statistic from the sample data.
Determine the Probability: Calculate the probability of observing a test statistic as extreme as, or more extreme than, the one obtained, under the assumption that the null hypothesis is true.

This probability is the p-value.

Interpreting P-values in Research Contexts

Consider a study comparing two teaching methods to determine which one is more effective and the p-value obtained from the analysis is 0.03.
Since 0.03 is less than the common alpha level of 0.05, the result is considered statistically significant, and the null hypothesis is rejected in favor of the alternative hypothesis.

Common Misconceptions About P-values

1. P-Value Indicates the Probability That the Null Hypothesis Is True

This is a common misunderstanding. The p-value does not provide the probability that the null hypothesis is true or false. Instead, it indicates the probability of obtaining the observed data, or more extreme, assuming the null hypothesis is true.

2. A Small P-Value Confirms a Large or Important Effect

A small p-value indicates statistical significance but does not measure the size or importance of an effect. It’s possible to have a statistically significant result with a negligible effect size, especially in large samples.

3. A P-Value Above 0.05 Means There Is No Effect

Failing to reject the null hypothesis (e.g., p-value > 0.05) does not prove that there is no effect. It may indicate insufficient evidence to detect an effect, possibly due to a small sample size or variability in the data.

Advantages of Using P-Values

1. Standardized Measure for Statistical Significance

The p-value offers a standardized method to assess whether observed data significantly deviate from what would be expected under the null hypothesis. This standardization facilitates consistent decision-making across various studies and disciplines.

2. Facilitates Hypothesis Testing

In hypothesis testing, the p-value helps determine the strength of evidence against the null hypothesis. A smaller p-value indicates stronger evidence to reject the null hypothesis, aiding researchers in drawing conclusions from their data.

3. Widely Accepted in Scientific Research

P-values are universally recognized in the scientific community, making them a common language for reporting and interpreting statistical results. Their widespread use allows for easier comparison and replication of studies.

4. Supports Regulatory and Policy Decisions

Regulatory bodies, such as the U.S. Food and Drug Administration (FDA), often rely on p-values to assess the efficacy and safety of new treatments. A statistically significant p-value can be a critical factor in the approval process of new drugs and interventions.

Limitations of P-Values

1. Does Not Measure Effect Size

A significant p-value indicates that an effect exists but does not convey the magnitude of that effect. Consequently, a study may find a statistically significant result with a negligible practical impact, especially in large samples.

2. Sensitive to Sample Size

P-values are influenced by the size of the sample. In large samples, even trivial effects can yield small p-values, leading to potentially misleading conclusions about the importance of findings.

3. Misinterpretation as Probability of Hypotheses

A common misconception is interpreting the p-value as the probability that the null hypothesis is true. In reality, the p-value assumes the null hypothesis is true and calculates the probability of observing the data, or something more extreme.

4. Does Not Account for Study Design Quality

P-values do not reflect the quality of the study design or data collection methods. A statistically significant result from a poorly designed study may not be reliable.

5. Risk of Multiple Comparisons Problem

Conducting multiple statistical tests increases the chance of obtaining a significant p-value purely by chance. Without proper adjustments, this can lead to false-positive findings.

Best Practices for Using and Reporting P-Values

1. Report Exact P-Values

Instead of stating that results are significant at p < 0.05, report the exact p-value (e.g., p = 0.032). This provides more precise information about the strength of the evidence against the null hypothesis.

2. Include Effect Sizes and Confidence Intervals

Effect sizes quantify the magnitude of the observed effect, while confidence intervals provide a range of values within which the true effect likely lies. Including these metrics alongside p-values offers a more comprehensive understanding of the results.

3. Consider study design and data quality

P-values should not be the sole determinant of research conclusions. Consider the study design, data quality, methodology, data collection process and other relevant factors to assess the reliability of the findings and interpreting the results.

4. Be Cautious and adjust Multiple Comparisons

Conducting multiple statistical tests increases the risk of Type I errors (false positives). Apply appropriate corrections (e.g., Bonferroni correction) when performing multiple comparisons.

5. Avoid Dichotomous Thinking: Rather than categorizing results as simply significant or not, interpret p-values as part of a continuum of evidence.

Alternatives and Complements to P-value

1. Confidence Intervals

Confidence intervals provide a range of values that likely contain the true effect size. They offer information about the precision and uncertainty of the estimate, which p-values alone do not convey.

2. Effect Sizes

Effect sizes measure the magnitude of an effect, providing context to the statistical significance indicated by p-values. Common effect size measures include Cohen’s d, Pearson’s r, and odds ratios.

3. Bayesian Methods

Bayesian statistics offer an alternative framework, allowing for the incorporation of prior knowledge and providing probabilities for hypotheses. This approach can offer more nuanced insights.

Conclusion

P-value is a valuable tool in statistical analysis, offering a standardized method for evaluating evidence against the null hypothesis. However, its limitations necessitate cautious interpretation and should be complemented with other statistical measures and a thorough understanding of the study context. By recognizing the limitations and proper applications, researchers can make more informed and reliable conclusions in their studies.