Z-Score and its Classification

June 9, 2017 Kusum Wagle Nutrition 0

Z-Score

Introduction

  • Z-score, also known as Standard Deviation (SD) score is the measure of dispersion/relative deviance of the data from the mean/median value i.e. measure of the distance between the child’s value and value of the reference population 

     Note: (Reference/sample populations are carefully selected/predetermined population which           represents the entire population of a certain area of particular age and sex groups)

  • It is a statistical measurement of a particular score’srelationship to the mean in a group of scores.
  • To make it more clear, a z-score of 0 of an individual means that the score of an individual is same as the mean score.
  • It can be both positive and negative which shows whether the particular score is greater (in case of +) or less (in case of -) than the score of sample population
  • It is also necessary to know that Z-score is a comparative score not the absolute value as the score of an individual/population is compared across the reference population
  • Z-score (or SD-score) = (observed value – median value of the reference population) / standard deviation value of reference population. More simply, Z- score= (Score-Mean) / SD
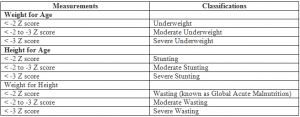
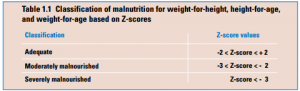
  • Z-score can be used in different fields wherever statistical measurement is required. However, in case of nutrition we usually calculate Z-score for weight-for-height, height-for-age and weight-for-age.
  • All these measurements of Z-score in nutrition give answer to the question that whether the child is malnourished or not and the range of malnutrition (mild/moderate/severe)

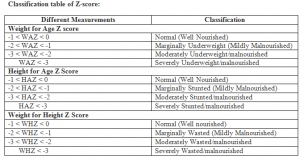
In other words,

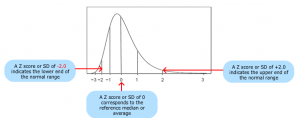
Looking at Z-score value through Normally distributed Bell curve:

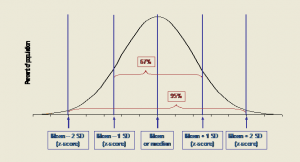
Advantages/usefulness of Z-score:

About Kusum Wagle 214 Articles
Hello and greetings everyone! I am Kusum Wagle, MPH, WHO-TDR Scholar, BRAC James P. Grant School of Public Health, Bangladesh. I have gained profound experiences in public health sector under different thematic areas of health, nutrition, sexual and reproductive health, maternal and newborn health, research etc., targeting diverse audience of different age groups. I have performed diverse roles ranging from lecturer in the public health department of colleges, nutrition coordinator, research coordinator and consultant, in different programs, projects and academic institutions of Nepal. I also hold immense experience in working closely and persistently with government organizations, non-government organizations, UN agencies, CSOs and other stakeholders at the national and sub-national level. I have successfully led and coordinated different projects involving multi-sector participation and engagement. Moreover, I am also regularly involved in the development of different national health related programs and its guidelines.