Linear Regression Vs Logistic Regression

Table of Contents

What is Regression?

Regression is a technique used to predict the value of a response (dependent) variables, from one or more predictor (independent) variables, where the variable is numeric. There are various forms of regression such as linear, multiple, logistic, polynomial, non-parametric, etc.

Linear regression:

Linear regression is a technique of regression analysis that establishes the relationship between two variables using a straight line.
It is used for predicting the continuous dependent variable on the basis of independent variables.
The purpose of Linear regression is to estimate the continuous dependent variable in case of a change in independent variables.
If single independent variable is used for prediction then it is called Simple Linear Regression and if there are two or more than two independent variables, then such regression is called as Multiple Linear Regression.
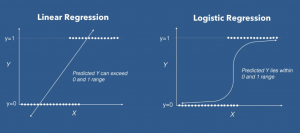
Output for linear regression must be a continuous value. E.g.: age, price etc.
Linear regression is used when the dependent variable is continuous (age, height, weight etc.)
Here, relationship between dependent variable and independent variable must be linear.
Using linear regression, collinearity between the independent variables can be identified.
Linear Regression includes fitting a straight line in the data
Linear regression assumes Gaussian (or normal) distribution of the dependent variable.
The purpose of Linear regression is to estimate the continuous dependent variable in case of a change in independent variables. For example, relationship between hours studied and marks in exam.
Application of Linear regression is based on Least Square Estimation Method.
Linear regression is of two types:
1. Simple Linear regression
2. Multiple Linear regression

Logistic Regression:

Logistic regression is a technique of regression analysis for analyzing a data set in which there are one or more independent variables that determine an outcome which is categorical.
Logistic regression is used when the dependent variable (y) is binary in nature.
Logistic regression helps in binary classification.
Application of logistic regression is based on Maximum Likelihood Estimation Method
Logistic Regression is about fitting a curve to the data.
The purpose of Logistic regression is to estimate the categorical dependent variable using a given set of independent variables. For example, logistic regression can be used to calculate the probability of an event. For example; an event can be whether it will rain tomorrow or not.
The dependent variables are categorical in nature. Logistic Regression is used for solving the classification problems.
In logistic regression, the relationship between dependent variable and independent variable is not necessarily required to be linear.
Logistic regression does not require error term to be distributed normally.
The output of logistic regression must be a categorical value. E.g.; Yes/No, 0/1, Red/Blue/Yellow etc.
In logistic regression, there should not be collinearity between the independent variables.
Logistic regression are of three types:
1. Binomial logistic regression
2. Multinomial logistic regression
3. Ordinal logistic regression

Major Differences Between Linear Regression and Logistic Regression:

Linear Regression	Logistic Regression
In linear regression, continuous dependent variable and the independent variables can be continuous or discrete.	In logistic regression, dependent variable should be categorical.
In linear regression, the dependent variable is continuous (age, height, weight etc.)	In logistic regression, the dependent variables are categorical in nature. (Yes/No, 0/1, True/False, Red/Yellow/Green)
The output for linear regression must be a continuous value such as age, price, weight etc.	The output value of logistic regression must be a categorical value such as 0 or 1, Yes or No.
Linear Regression is a supervised regression model.	Logistic Regression is a supervised classification model.
The purpose of Linear regression is to estimate the continuous dependent variable in case of a change in independent variables.	The purpose of Logistic regression is to estimate the categorical dependent variable using a given set of independent variables.
No activation function is required	Activation function is required to convert linear regression equation to logistic regression equation.
Linear regression includes fitting a straight line in the data	Logistic regression includes fitting a curve to the data. Any change in the coefficient leads to change in both direction and steepness of the logistic function. Positive slopes result in S-curve while negative slopes result in Z-curve.
Relationship between dependent and independent variables must be linear.	Relationship between dependent and independent variables should not be necessarily linear.
It assumes normal or Gaussian distribution of dependent variable.	It assumes binomial distribution of dependent variable.
Interpretation of the coefficient of linear regression is simple.	Interpretation of the coefficient of logistic regression is quite complex as it depends on log, inverse-log, binomial etc.
Independent variables can be correlated with one another.	Variables must not be correlated with one another.
Application of Linear regression is based on Least Square Estimation Method	Application of logistic regression is based on Maximum Likelihood Estimation Method
Least square estimation method is used to minimize errors between the actual values and the predicted values.	Maximum likelihood estimation method is used to minimize errors.
It requires error term to be distributed normally.	It does not require error term to be distributed normally.
Sample size: Linear regression requires at least 5 cases per independent variable to perform the analysis.	Sample size: Logistic regression requires at least 10 events per independent variable to perform the analysis.